Higher Order Euclidean Sets, or
Hypereuclidean Sets

Back to Home Page
SMT Paper
Jacksonville, FL | 10 November, 2024
View the Paper | View the Presentation
Summary
The idea of higher-order Euclidean sets (also referred to as "hypereuclidean sets") builds upon research by Godfried Toussaint, John Clough, Jack Douthett and others. A higher-order set is created by taking a series of related Euclidean sets and using those with lower n-values as index sets. Elements from higher-order sets are removed recursively by lower-order elements. In this way, the method can generate interrelated structures that have a greater variety of IOIs (inter-onset-intervals) than conventional Euclidean sets. Higher-order sets are essentially the same as second-order or "deeper-order" maximally-even sets. Analysis can potentially show relationships among very different musical structures by charting shared lineages.

The problem of creating, finding and relating higher-order Euclidean sets lies principally in the sheer quantity of sets that the algorithm produces. Further complications arise in sorting, identifying interesting properties, and relating sets to musical structures. There are solutions to all these challenges. The method is worth the effort because it produces musically rich results, and it can be applied either to rhythm or pitch.

To better understand the principles, I have written two patches in Max/MSP that vividly illustrate the technique of creating higher-order Euclidean sets in a simple and visually intuitive way. While Max offers an appealing environment for casual exploration, its scheduler is not designed for computationally intensive tasks, so it is best for generating one set at a time.

To do the heavy lifting of generating many higher-order Euclidean sets, I wrote a pair of C++ programs that run on the command line. Two programs are available. The first prompts the user for all the relevant information, and generates a single set. This program is intended for targeted searches. The other program only prompts the user for the outer bounds, and generates a family of sets in a way that seeks to achieve some measure of algorithmic optimization.

Additional algorithms find the standard deviations of the generated sets' IOIs, and count the number of occurrences of each unique onset pattern in the potentially very large family of generated sets.

Release Notes & Downloads
All the code is available for free on GitHub. You can obtain it here: https://github.com/lauprellim/euclid. Note that there is a main branch and a development branch. The programs in the development branch have all been tested and should compile (though there may be a warning or two). The code was written on a Raspberry Pi 5 running Debian in Microsoft Visual Studio.

The Max/MSP patches have been tested on Max 8.6, but not Max 9.0. They require the free Bach and Cage libraries. Please be sure these libraries are installed or the patches won't work. You can easily get them through Max's Package Manager. The patches also have three dependencies, namely two JavaScript files and a .json file which stores the presets. These are part of the .zip file. Be sure the patcher can access them.

All C++ programs are available as source code. After compilation, users can easily write the output of both programs to text files using the command line (pipe tee), and then search for sets using grep. Future plans may include organizing the output of the "make-many" C++ program into trees, and other tools to organize the generated material.

I'm sure I could optimize the C++ source in many ways. I'd be glad to receive whatever feedback the community might offer. This is an ongoing project.
Music made using higher-order Euclidean sets
  • A very simple example using only a first-order Euclidean set, created with Ableton Live 12's built-in tools.
  • A composition etude using a family of five hypereuclidean sets with n=128.
  • New Clapping Music -- an amusing hypereuclidean take on a famous rhythm cycle

Algorithmic Performance
Run on a 2.4 GHz Quad-Core Intel Core i5 MacBook Pro (2019!)
depth n kn # of sets computation time
1 12 3 12 N/A
2 12 3 1152 0.050889 sec
3 12 3 48,384 2.87007 sec
4 12 3 1,161,216 101.972 sec
Some screen shots
Generating Steve Reich's "Clapping Music" as a second-order Euclidean set using the subtract-first method



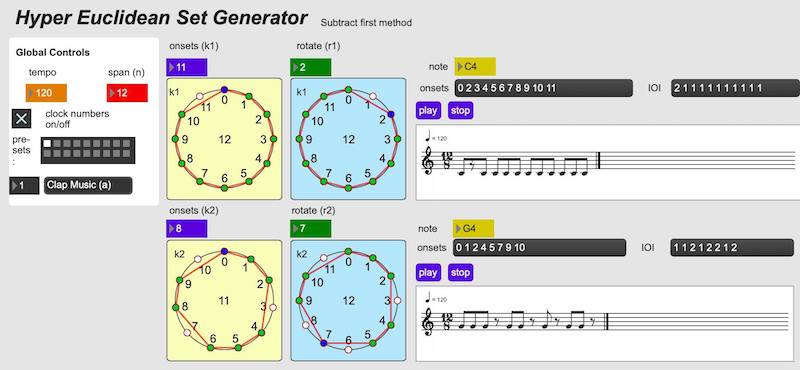
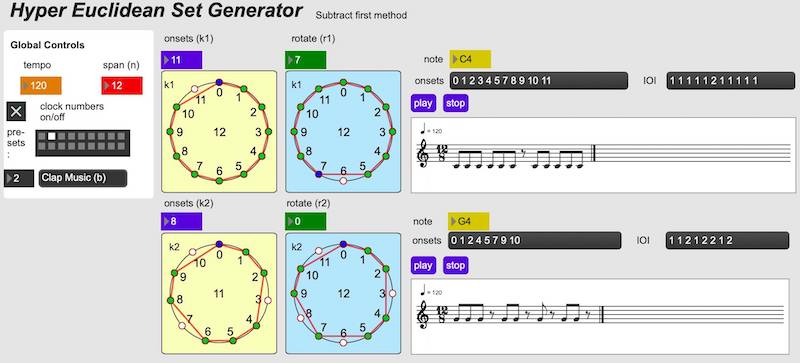
Partial Bibliography

Burke, Richard (submitted by L. Poundie Burstein, June 2015). “’That Awkward Scale’: Verdi, Puccini and the Scala enigmatica.” Music Theory Online 21.2. Online

Carey, Norman and David Clampitt (1989). "Aspects of Well-Formed Scales". Music Theory Spectrum 11/2, 187–206.

Clough, John and Jack Douthett (Spring - Autumn 1991). “Maximally Even Sets.” Journal of Music Theory 35.1/2, 93–173.

Clough, John and Gerald Myerson (1985). "Variety and Multiplicity in Diatonic Systems", Journal of Music Theory 29/2, 249-270.

Cohn, Richard (1992). “Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase-Shifting Music.” Perspectives of New Music 30/2, 146–77.

Condit-Schultz, Nathaniel (2019). "Deconstructing the nPVI: A Methodological Critique of the Normalized Pairwise Variability Index as Applied to Music", Music Perception 36/3, 300-313.

Danielsen, Ann, Mats Johansson, Chris Stover (2023). "Bins, Spans, and Tolerance: Three Theories of Microtiming Behavior", Music Theory Spectrum 45/2, (Fall 2023), 181–198.

Demaine, Erik D. et al. (2009). “The Distance Geometry of Music.” Computational Geometry 42.5, 429–454.

Johnson, Timothy (2003). Foundations of Diatonic Theory: A Mathematical Based Approach to Musical Fundamentals. Key College Publishing.

Gómez-Martin, Francisco, Perouz Taslakian, and Godfried Toussaint (Apr. 2009a). “Interlocking and Euclidean Rhythms.” Journal of Mathematics and Music 3.1, 15–30.

—---- (2009b). “Structural Properties of Euclidean Rhythms.” Journal of Mathematics and Music 3.1, 1–14.

Gotham, Mark (2013). "Review of Godfried Toussaint, The Geometry of Musical Rhythm: What Makes a 'Good' Rhythm Good?", Music Theory Online 19/2. Online

Hall, Rachel W. and Paul Klingsberg (Dec. 2006). “Asymmetric Rhythms, Tiling Canons, and Burnside’s Lemma.” The American Mathematical Monthly 113.10, 887–896.

London, Justin (2004). Hearing in Time: Psychological Aspects of Musical Meter. Oxford: Oxford University Press.

Osborn, Brad (Winter 2014). “Kid Algebra: Radiohead’s Euclidean and Maximally Even Rhythms.” Perspectives of New Music 52.1, 81–105.

-----. (2017). Everything in its Right Place: Analyzing Radiohead. New York: Oxford University Press.

Pearsall, Edward (1997). “Interpreting Music Durationally: A Set-Theory Approach to Rhythm.” Perspectives of New Music 35/1, 205–30.

Pressing, Jeff (1983). “Cognitive Isomorphisms between Pitch and Rhythm in World Musics: West Africa, the Balkans and Western Tonality.” Studies in Music 17, 38–61.

Rahn, Jay (1987). "Asymmetrical ostinatos in sub-Saharan music: Time, pitch, and cycles reconsidered." In Theory Only 9 (7), 23-27.

Toussaint, Godfried (2005). “The Euclidean Algorithm Generates Traditional Musical Rhythms.” Online

—---- (2012). “The pairwise variability index as a tool in musical rhythm analysis.” Proceedings of the 12th International Conference on Music Perception, Cognition (ICMPC), and 8th Trienniel Conference of the European Society for the Cognitive Sciences of Music (ESCOM). Thessaloniki, Greece. Online

—---- (2020). The Geometry of Musical Rhythm. 2nd ed. CRC Press (Taylor Francis Group).

Tymoczko, Dmitri (2011). A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.

Yeston, Maury (1976). The Stratification of Musical Rhythm. New Haven: Yale University Press.
Last updated on 9 November 2024.
Content on this page is licenced under GNU General Public License.